Algorithm Design Manual - Booknotes
Arrays:
Constant-time access, given an index
Space efficiency
Memory locality
Constant-time access, given an index
Space efficiency
Memory locality
Linked Lists:
No overflows (unless memory is physically full)
Simpler insertions & deletions
Requires space for pointers
No efficient random access
No overflows (unless memory is physically full)Simpler insertions & deletions
Requires space for pointers
No efficient random access
Stacks
LIFO: Push, Pop operations
LIFO: Push, Pop operations
Queues
FIFO: Queue, Dequeue operations
FIFO: Queue, Dequeue operations
Dictionaries
Permits access by content
Search, Insert, Delete operations
Max, Min, Predecessor, Successor operations (some types of Dicts)
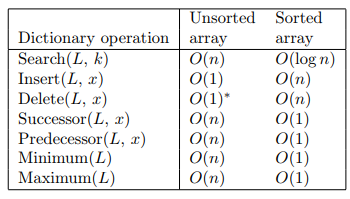
Array operation costs - unsorted vs sorted:
Permits access by content
Search, Insert, Delete operations
Max, Min, Predecessor, Successor operations (some types of Dicts)
Array operation costs - unsorted vs sorted:
Dictionary operation costs - sorted/unsorted, single/double links: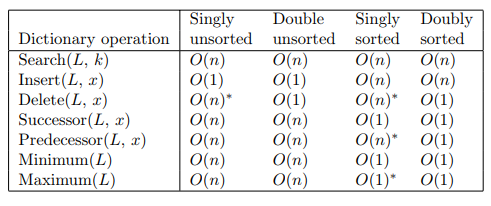
Binary Search Trees
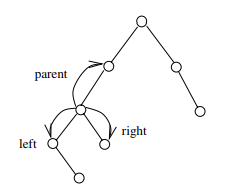
Search, Min element, Max element, Traverse (all elements), Insert, Delete operations
Ops can take O(height) time if tree is perfectly balanced. But insertions can cause trees to be unbalanced very easily.
Ops can take O(height) time if tree is perfectly balanced. But insertions can cause trees to be unbalanced very easily.
Priority Queues
Allows new elements to be placed at arbitrary intervals = more flexibility.
Allows new elements to be placed at arbitrary intervals = more flexibility.
Hash:
A math function that maps keys to integers. Use hash outputs as array indexes.
Collisions
Two distinct keys can return identical hash values.
Chaining:
m Most common way to resolve collisions. Natural solution, but uses lots of pointer memory.
A math function that maps keys to integers. Use hash outputs as array indexes.
Collisions
Two distinct keys can return identical hash values.
Chaining:
m Most common way to resolve collisions. Natural solution, but uses lots of pointer memory.
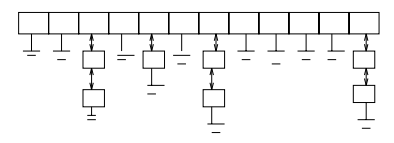
Open Addressing: if desired position is already occupied, use another position (often n+1 or n-1)
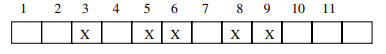
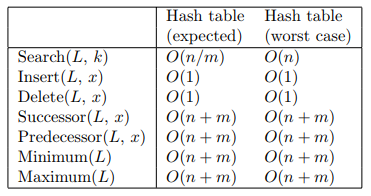
Operation times (m-element hash table, doubly-linked chain lists)
